euler tour of a graph

Eulerian Cycle

An Eulerian cycle, also called an Eulerian circuit, Euler circuit, Eulerian tour, or Euler tour, is a trail which starts and ends at the same graph vertex . In other words, it is a graph cycle which uses each graph edge exactly once. For technical reasons, Eulerian cycles are mathematically easier to study than are Hamiltonian cycles . An Eulerian cycle for the octahedral graph is illustrated above.

As a generalization of the Königsberg bridge problem , Euler showed (without proof) that a connected graph has an Eulerian cycle iff it has no graph vertices of odd degree .

Fleury's algorithm is an elegant, but inefficient, method of generating an Eulerian cycle. An Eulerian cycle of a graph may be found in the Wolfram Language using FindEulerianCycle [ g ].

Explore with Wolfram|Alpha

More things to try:

• acyclic graph
• (1 - 1/3 + 1/5) / (1/2 - 1/4 + 1/6)

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Eulerian Cycle." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/EulerianCycle.html

Subject classifications

Reset password New user? Sign up

Existing user? Log in

Eulerian Path

Already have an account? Log in here.

An Eulerian path on a graph is a traversal of the graph that passes through each edge exactly once, and the study of these paths came up in their relation to problems studied by Euler in the 18th century like the one below:

Is there a walking path that stays inside the picture and crosses each of the bridges exactly once?

After trying and failing to draw such a path, it might seem plausible that the task is impossible. But how can this be proven? What if the configuration of bridges is slightly different? (For instance, it is not hard to cross all but one of the bridges, and adding another bridge to the existing seven would also allow a complete crossing.) Is there a way to characterize the configurations that allow for these paths? What if the path is required to start and end at the same place?

The answers to these questions were first supplied in 1736, by Leonhard Euler , in a paper that proved the first result in what is now known as graph theory . Paths traversing all the bridges (or, in more generality, paths traversing all the edges of the underlying graph) are known as Eulerian paths , and Eulerian paths which start and end at the same place are called Eulerian circuits .

The problem above is known as the Bridges of Konigsberg problem, named after a city in Prussia on the Pregel River with bridges configured as in the picture.

An informal proof

Graphs, eulerian paths, and eulerian circuits, fleury's algorithm, proof of the theorem, bridges of konigsberg revisited, five-room puzzle.

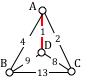
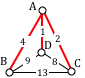
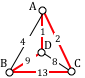
There are four landmasses in the picture. Every path that crosses the bridges will go back and forth between these four landmasses. Suppose there is a person standing on each landmass and watching someone walking the path, counting every time the walker either enters or exits the landmass (including the beginning and end of the path in their count). If there is a path that crosses each bridge exactly once, what will the counters' numbers be when the walker finishes?

The counter on the top will have \( 3 \), since each of the three bridges that hits his landmass will have been crossed exactly once, and each crossing will be counted as either an entry or an exit. Similarly, the counter on the middle island will show \( 5 \), the counter on the right will show \( 3\), and the counter at the bottom will show \( 3 \).

But the walker enters and exits each landmass every time he passes through, which contributes \( 2 \) to the count, so each counter's final count should be an even number--except for the two counters who count the beginning and the end of the path (the first exit doesn't have a corresponding entry, and the last entry doesn't have a corresponding exit). Still, it's impossible for all four counters to end with odd numbers, so there is no such path.

This problem can be rephrased in terms of graph theory , as follows. Consider the graph with vertices corresponding to the four landmasses, and edges between the vertices corresponding to the bridges. The path in question is a traversal of the graph that passes through each edge exactly once. Or, in other words, it is a drawing of the graph on a piece of paper without picking up our pencil or drawing any edge more than once.

In what follows, graphs will be assumed to be finite (with finitely many vertices and edges). Recall that the degree of a vertex in a graph is the number of edges that touch the vertex.

Here is the graph that corresponds to the bridge problem.

The degree of a vertex corresponding to one of the four landmasses in the original problem is the number that each counter will have in the above proof: the top, right, and bottom vertices have degree \( 3 \) and the left vertex has degree \( 5 \).

An Eulerian path on a graph is a traversal of the graph that passes through each edge exactly once. It is an Eulerian circuit if it starts and ends at the same vertex. \(_\square\)

The informal proof in the previous section, translated into the language of graph theory, shows immediately that:

If a graph admits an Eulerian path, then there are either \( 0 \) or \( 2 \) vertices with odd degree. If a graph admits an Eulerian circuit, then there are \( 0 \) vertices with odd degree.

The more interesting and difficult statement is the converse. What conditions guarantee the existence of an Eulerian path or Eulerian circuit? It turns out that aside from the necessary conditions on degrees, the only other requirement is the obvious one that any two vertices of degree \(\ge 1\) have a path between them.

A graph is connected if there is a path between any two vertices. \(_\square\)

Every (finite) graph can be uniquely decomposed into connected components : each component is a connected subgraph, and there are no edges between any two components. A vertex of degree zero is its own connected component.

A graph has an Eulerian path if and only if (1) every vertex of degree \(\ge 1\) lies in the same connected component, and (2) there are 0 or 2 vertices of odd degree. A graph has an Eulerian circuit if and only if (1) every vertex of degree \(\ge 1\) lies in the same connected component, and (2) every vertex has even degree. \(_\square\)

Euler stated this theorem without proof when he solved the Bridges of Konigsberg problem in 1736, but the proof was not given until the late \(19^\text{th}\) century.

Can we color the edges of the octahedron above without lifting the pencil nor coloring the same edge more than once?

Define the cube graph \( C_n \) as follows:

There are \( 2^n \) vertices, labelled \( v_0, v_1, \ldots, v_{2^n-1} \). Draw an edge between \( v_a \) and \( v_b\) if and only if the binary representations of \( a \) and \( b\) differ in exactly one digit.

We would like to find a path along the cube graph \( C_n \) that crosses each edge exactly once, and begins and ends at the same vertex. For \( C_2 \) this is possible: start at 0, move to 2, move to 3, move to 1, move back to 0.

What about for \( n = 3 \) or \( n = 4 ? \)

To prove the theorem, the "only if" statements have been established by the above discussion. One way to prove the "if" statements is via the following algorithm due to Fleury which constructs an Eulerian path or circuit.

If there are two vertices of odd degree, start with one of them. Otherwise, start with any vertex. At every step of the algorithm, pick an edge that will not disconnect the graph if it is removed, unless there is no such edge. (Edges that will disconnect the graph if they are removed are--somewhat confusingly in this context--called bridges .) Move along this edge and delete it from the graph once done. Continue.

Every graph has an even number of vertices with odd degree.

Proof: Every edge hits two vertices, so the sum of the degrees of the vertices equals twice the number of edges. So it is even. The lemma follows immediately.

Rather than giving the details of this proof, here is an alternative algorithm due to Hierholzer that also works. The algorithm produces Eulerian circuits, but it can be modified to produce Eulerian paths if there are two vertices of odd degree.

Suppose every vertex has even degree. Start with a vertex \( v \) and follow a path around the graph until it returns to \( v\). This will always be possible because there will always be an odd number of unused edges emanating from a vertex that the path has landed on. This produces a circuit that may not be Eulerian; but if it is not, we can start from a vertex \(w\) with some unused edges coming from it and follow a path of unused edges around the graph until it returns to \( w \). The old circuit plus the new one can be traversed as one large circuit (start at \( v\), go to \( w\), do the \( w\) circuit, continue the rest of the \( v\) circuit). Repeat until there are no more unused edges. \( \square\)

A graph in which all vertices have even degree. [1] Consider the above graph. Starting at vertex 1, draw a circuit 1-2-3-7-1. There are unused edges emanating from vertex 1, so draw another circuit 1-3-4-7-8-1. Put them together to get 1-2-3-7-1-3-4-7-8-1. Now vertex 1 no longer has unused edges, but vertex 4 does: draw 4-5-9-4. Stick this into the previous circuit to get \[ 1-2-3-7-1-3-{\bf 4-5-9-4}-7-8-1. \] Finally, vertex 9 has some unused edges left, so draw the circuit 9-6-7-9 and notice that all the edges have been used. Stick it into the previous circuit to get \[ 1-2-3-7-1-3-4-5-{\bf 9-6-7-9}-4-7-8-1. \]

The Konigsberg bridges have the interesting property that adding or deleting a bridge between any two landmasses will allow an Eulerian path. Indeed, adding or deleting a bridge will change the parity of the degrees of two of the four vertices of the associated graph, which will make them both even. Then there will be two vertices of odd degree, which will imply the existence of an Eulerian path.

This illustrates the power of the theorem; without having to draw the paths in all of the various cases that might arise, nevertheless an affirmative answer can be given to the question of the existence of Eulerian paths.

Another application of the theorem is to the following puzzle:

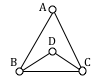
Suppose five rooms in a house are laid out as follows: Imagine a door cut into each wall of each room (including the outside). Is there a path that goes through each door exactly once? The answer is no, as the associated graph has four vertices of odd degree. Here are the graphs for the Konigsberg and five-room problems, respectively, with degrees pictured on each vertex. Note that it is possible in the five-room problem to construct a path that passes through all but one door, but in this case only certain doors can be omitted; the door has to correspond to an edge connecting two odd-degree vertices. \(_\square\)

• Tin Tin, C. Hierholzer's algorithm . Retrieved August 8, 2008, from https://commons.wikimedia.org/wiki/File:Hierholzer_(3).png

Problem Loading...

Note Loading...

Set Loading...

Finding the Eulerian path in $O(M)$ ¶

A Eulerian path is a path in a graph that passes through all of its edges exactly once. A Eulerian cycle is a Eulerian path that is a cycle.

The problem is to find the Eulerian path in an undirected multigraph with loops .

Algorithm ¶

First we can check if there is an Eulerian path. We can use the following theorem. An Eulerian cycle exists if and only if the degrees of all vertices are even. And an Eulerian path exists if and only if the number of vertices with odd degrees is two (or zero, in the case of the existence of a Eulerian cycle). In addition, of course, the graph must be sufficiently connected (i.e., if you remove all isolated vertices from it, you should get a connected graph).

To find the Eulerian path / Eulerian cycle we can use the following strategy: We find all simple cycles and combine them into one - this will be the Eulerian cycle. If the graph is such that the Eulerian path is not a cycle, then add the missing edge, find the Eulerian cycle, then remove the extra edge.

Looking for all cycles and combining them can be done with a simple recursive procedure:

The complexity of this algorithm is obviously linear with respect to the number of edges.

But we can write the same algorithm in the non-recursive version:

It is easy to check the equivalence of these two forms of the algorithm. However, the second form is obviously faster, and the code will be much more efficient.

The Domino problem ¶

We give here a classical Eulerian cycle problem - the Domino problem.

There are $N$ dominoes, as it is known, on both ends of the Domino one number is written(usually from 1 to 6, but in our case it is not important). You want to put all the dominoes in a row so that the numbers on any two adjacent dominoes, written on their common side, coincide. Dominoes are allowed to turn.

Reformulate the problem. Let the numbers written on the bottoms be the vertices of the graph, and the dominoes be the edges of this graph (each Domino with numbers $(a,b)$ are the edges $(a,b)$ and $(b, a)$ ). Then our problem is reduced to the problem of finding the Eulerian path in this graph.

Implementation ¶

The program below searches for and outputs a Eulerian loop or path in a graph, or outputs $-1$ if it does not exist.

First, the program checks the degree of vertices: if there are no vertices with an odd degree, then the graph has an Euler cycle, if there are $2$ vertices with an odd degree, then in the graph there is only an Euler path (but no Euler cycle), if there are more than $2$ such vertices, then in the graph there is no Euler cycle or Euler path. To find the Euler path (not a cycle), let's do this: if $V1$ and $V2$ are two vertices of odd degree, then just add an edge $(V1, V2)$ , in the resulting graph we find the Euler cycle (it will obviously exist), and then remove the "fictitious" edge $(V1, V2)$ from the answer. We will look for the Euler cycle exactly as described above (non-recursive version), and at the same time at the end of this algorithm we will check whether the graph was connected or not (if the graph was not connected, then at the end of the algorithm some edges will remain in the graph, and in this case we need to print $-1$ ). Finally, the program takes into account that there can be isolated vertices in the graph.

Notice that we use an adjacency matrix in this problem. Also this implementation handles finding the next with brute-force, which requires to iterate over the complete row in the matrix over and over. A better way would be to store the graph as an adjacency list, and remove edges in $O(1)$ and mark the reversed edges in separate list. This way we can archive a $O(N)$ algorithm.

Practice problems: ¶

• CSES : Mail Delivery
• CSES : Teleporters Path
• singamandeep (88.48%)
• anishagg17 (3.03%)
• adamant-pwn (2.42%)
• jakobkogler (1.21%)
• svaderia (1.21%)
• Aryamn (1.21%)
• beingnoble03 (0.61%)
• sohaibuddinsyed (0.61%)
• apupneja (0.61%)
• algmyr (0.61%)

• 1 Definitions
• 2 Necessary and sufficient conditions
• 3 Fleury's algorithm
• 4.1 Pseudocode
• 5 Generalizations
• 6 Python implementation

Definitions [ edit ]

An Euler tour (or Eulerian tour) in an undirected graph is a tour that traverses each edge of the graph exactly once. Graphs that have an Euler tour are called Eulerian .

Some authors use the term "Euler tour" only for closed Euler tours.

Necessary and sufficient conditions [ edit ]

An undirected graph has a closed Euler tour iff it is connected and each vertex has an even degree.

An undirected graph has an open Euler tour (Euler path) if it is connected, and each vertex, except for exactly two vertices, has an even degree. The two vertices of odd degree have to be the endpoints of the tour.

A directed graph has a closed Euler tour iff it is strongly connected and the in-degree of each vertex is equal to its out-degree.

Similarly, a directed graph has an open Euler tour (Euler path) iff for each vertex the difference between its in-degree and out-degree is 0, except for two vertices, where one has difference +1 (the start of the tour) and the other has difference -1 (the end of the tour) and, if you add an edge from the end to the start, the graph is strongly connected.

Fleury's algorithm [ edit ]

Fleury's algorithm is a straightforward algorithm for finding Eulerian paths/tours. It proceeds by repeatedly removing edges from the graph in such way, that the graph remains Eulerian. A version of the algorithm, which finds Euler tour in undirected graphs follows.

Start with any vertex of non-zero degree. Choose any edge leaving this vertex, which is not a bridge (i.e. its removal will not disconnect the graph into two or more disjoint connected components). If there is no such edge, stop. Otherwise, append the edge to the Euler tour, remove it from the graph, and repeat the process starting with the other endpoint of this edge.

Though the algorithm is quite simple, it is not often used, because it needs to identify bridges in the graph (which is not a trivial thing to code.) Slightly more sophisticated, but easily implementable algorithm is presented below.

Cycle finding algorithm [ edit ]

This algorithm is based on the following observation: if C is any cycle in a Eulerian graph, then after removing the edges of C, the remaining connected components will also be Eulerian graphs.

The algorithm consists in finding a cycle in the graph, removing its edges and repeating this steps with each remaining connected component. It has a very compact code with recursion:

Pseudocode [ edit ]

This algorithm can also be used to find Eulerian paths: simply connect the path's endpoints by a dummy edge, and find Euler tour.

Generalizations [ edit ]

In some practical situations, it is desirable to find a cycle, which visits all edges of a graph, when the graph does not have an Euler tour. In this case some of the edges will have to be visited more than once. If the graph is weighted, and a minimum-cost such cycle is sought, then this is what is known as a Chinese Postman Problem .

It's possible to generalize Euler tours to the case of mixed graphs, which contain both directed and undirected edges. See article UVa_10735 for a description of one possible algorithm for such graphs.

Python implementation [ edit ]

This is a short implementation of the Euler tour in python.

• Graph Theory

Navigation menu

T he motivation of this section is derived from the famous Konigsberg bridge problem solved by Leonhard Euler in 1736. The 18th century German city of K�nigsberg was situated on the river Pregel. Within a park built on the banks of the river, there were two islands joined by seven bridges. The puzzle asks whether it is possible to take a tour through the park, crossing each bridge only once.

An exhaustive search requires starting at every possible point and traversing all the possible paths from that point - an O(n!) problem. However Euler showed that an Eulerian path existed if and only if

• it is possible to go from any vertex to any other by following the edges (the graph must be connected) and
• every vertex must have an even number of edges connected to it, with at most two exceptions (which constitute the starting and ending points).

It is easy to see that these are necessary conditions: to complete the tour, one needs to enter and leave every point except the start and end points. The proof that these are sufficient conditions may be found in the literature . Thus we now have a O(n) problem to determine whether a path exists.

In order to get a solution transform the map into a graph in which the nodes represent the "dry land" points and the arcs represent the bridges.  

We can now easily see that the Bridges of K�nigsberg does not have a solution. A quick inspection shows that it does have a Hamiltonian path.

Definition     A Euler tour of a connected, directed graph G = (V, E) is a cycle that traverses each edge of graph G exactly once, although it may visit a vertex more than once.

In the first part of this section we show that G has an Euler tour if and only if in-degrees of every vertex is equal to out-degree vertex. In the second part, we describe an algorithm to find an Euler tour of graph if one exists.

Part 1    Show that G has an Euler tour if and only if in-degree( v ) = out-degree( v ) for each vertex v � V

First we'll work with => direction. We will call a cycle simple if it visits each vertex no more than once, and complex if can visit a vertex more than once. We know that each vertex in a simple cycle in-degree and out-degree one, and any complex cycles can be expressed as a union of simple cycles. This implies that any vertex in a complex cycle (and in particular an Euler tour) has in-degree equal to its out-degree. Thus, if a graph has an Euler tour than all of its vertices have equal in- and out- degrees.

Now look at the <= direction.

Suppose we have a connected graph for which the in-degree and out-degree of all vertices are equal. Let C be the longest complex cycle within G. If C is not an Euler tour, then there is a vertex v of G touched by C such that not all edges in and out v of are exhausted by C. We may construct a cycle C` in G-C starting and ending at v by performing a walk in G-C. (The reason is that G-C also has a property that in-degrees and out-degrees are equal.) this simply means that the complex cycle that starts at v goes along the edges of C` (returning to v ) and then goes along the edges of C is a longer complex cycle than C. This contradicts our choice of C as the longest complex cycle which means that C must have been an Euler tour.

Part 2 Find an Euler tour of given graph G if one exists.

Given a starting vertex , the v 0 algorithm will first find a cycle C starting and ending at  v 0 such that C contains all edges going into and out of  v 0 . This can be performed by a walk in the graph. As we discover vertices in cycle C, we will create a linked list which contains vertices in order and such that the list begins and ends in vertex  v 0 . We set the current painter to the head of the list. We now traverse the list by moving our pointer "current" to successive vertices until we and a vertex which has an outgoing edge which has not been discovered. (If we reach the end of the list, then we have already found the Euler tour). Suppose we find the vertex,  v i , that has an undiscovered outgoing edge. We then take a walk beginning and ending at  v i such that all undiscovered edges containing v i are contained in the walk. We insert our new linked list into old linked list in place of v i and more "current" to the new neighbor pointed to the first node containing v i . We continue this process until we search the final node of the linked list, and the list will then contains an Euler tour.

Running Time of Euler Tour

The algorithm traverse each edge at most twice, first in a walk and second while traversing the list to find vertices with outgoing edges. Therefore, the total running time of the algorithm is O(|E|) .

Discrete Mathematics An Open Introduction

Oscar Levin

Section 4.4 Euler Paths and Circuits

Investigate 35.

An Euler path , in a graph or multigraph, is a walk through the graph which uses every edge exactly once. An Euler circuit is an Euler path which starts and stops at the same vertex. Our goal is to find a quick way to check whether a graph (or multigraph) has an Euler path or circuit.

Which of the graphs below have Euler paths? Which have Euler circuits?

List the degrees of each vertex of the graphs above. Is there a connection between degrees and the existence of Euler paths and circuits?

Is it possible for a graph with a degree 1 vertex to have an Euler circuit? If so, draw one. If not, explain why not. What about an Euler path?

What if every vertex of the graph has degree 2. Is there an Euler path? An Euler circuit? Draw some graphs.

Below is part of a graph. Even though you can only see some of the vertices, can you deduce whether the graph will have an Euler path or circuit?

If we start at a vertex and trace along edges to get to other vertices, we create a walk through the graph. More precisely, a walk in a graph is a sequence of vertices such that every vertex in the sequence is adjacent to the vertices before and after it in the sequence. If the walk travels along every edge exactly once, then the walk is called an Euler path (or Euler walk ). If, in addition, the starting and ending vertices are the same (so you trace along every edge exactly once and end up where you started), then the walk is called an Euler circuit (or Euler tour ). Of course if a graph is not connected, there is no hope of finding such a path or circuit. For the rest of this section, assume all the graphs discussed are connected.

The bridges of Königsberg problem is really a question about the existence of Euler paths. There will be a route that crosses every bridge exactly once if and only if the graph below has an Euler path:

This graph is small enough that we could actually check every possible walk that does not reuse edges, and in doing so convince ourselves that there is no Euler path (let alone an Euler circuit). On small graphs which do have an Euler path, it is usually not difficult to find one. Our goal is to find a quick way to check whether a graph has an Euler path or circuit, even if the graph is quite large.

One way to guarantee that a graph does not have an Euler circuit is to include a “spike,” a vertex of degree 1.

The vertex \(a\) has degree 1, and if you try to make an Euler circuit, you see that you will get stuck at the vertex. It is a dead end. That is, unless you start there. But then there is no way to return, so there is no hope of finding an Euler circuit. There is however an Euler path. It starts at the vertex \(a\text{,}\) then loops around the triangle. You will end at the vertex of degree 3.

You run into a similar problem whenever you have a vertex of any odd degree. If you start at such a vertex, you will not be able to end there (after traversing every edge exactly once). After using one edge to leave the starting vertex, you will be left with an even number of edges emanating from the vertex. Half of these could be used for returning to the vertex, the other half for leaving. So you return, then leave. Return, then leave. The only way to use up all the edges is to use the last one by leaving the vertex. On the other hand, if you have a vertex with odd degree that you do not start a path at, then you will eventually get stuck at that vertex. The path will use pairs of edges incident to the vertex to arrive and leave again. Eventually all but one of these edges will be used up, leaving only an edge to arrive by, and none to leave again.

What all this says is that if a graph has an Euler path and two vertices with odd degree, then the Euler path must start at one of the odd degree vertices and end at the other. In such a situation, every other vertex must have an even degree since we need an equal number of edges to get to those vertices as to leave them. How could we have an Euler circuit? The graph could not have any odd degree vertex as an Euler path would have to start there or end there, but not both. Thus for a graph to have an Euler circuit, all vertices must have even degree.

The converse is also true: if all the vertices of a graph have even degree, then the graph has an Euler circuit, and if there are exactly two vertices with odd degree, the graph has an Euler path. To prove this is a little tricky, but the basic idea is that you will never get stuck because there is an “outbound” edge for every “inbound” edge at every vertex. If you try to make an Euler path and miss some edges, you will always be able to “splice in” a circuit using the edges you previously missed.

Euler Paths and Circuits

A graph has an Euler circuit if and only if the degree of every vertex is even.

A graph has an Euler path if and only if there are at most two vertices with odd degree.

Since the bridges of Königsberg graph has all four vertices with odd degree, there is no Euler path through the graph. Thus there is no way for the townspeople to cross every bridge exactly once.

Subsection Hamilton Paths

Suppose you wanted to tour Königsberg in such a way where you visit each land mass (the two islands and both banks) exactly once. This can be done. In graph theory terms, we are asking whether there is a path which visits every vertex exactly once. Such a path is called a Hamilton path (or Hamiltonian path ). We could also consider Hamilton cycles , which are Hamliton paths which start and stop at the same vertex.

Example 4.4.1

Determine whether the graphs below have a Hamilton path.

The graph on the left has a Hamilton path (many different ones, actually), as shown here:

The graph on the right does not have a Hamilton path. You would need to visit each of the “outside” vertices, but as soon as you visit one, you get stuck. Note that this graph does not have an Euler path, although there are graphs with Euler paths but no Hamilton paths.

It appears that finding Hamilton paths would be easier because graphs often have more edges than vertices, so there are fewer requirements to be met. However, nobody knows whether this is true. There is no known simple test for whether a graph has a Hamilton path. For small graphs this is not a problem, but as the size of the graph grows, it gets harder and harder to check wither there is a Hamilton path. In fact, this is an example of a question which as far as we know is too difficult for computers to solve; it is an example of a problem which is NP-complete.

Subsection Exercises

You and your friends want to tour the southwest by car. You will visit the nine states below, with the following rather odd rule: you must cross each border between neighboring states exactly once (so, for example, you must cross the Colorado-Utah border exactly once). Can you do it? If so, does it matter where you start your road trip? What fact about graph theory solves this problem?

This is a question about finding Euler paths. Draw a graph with a vertex in each state, and connect vertices if their states share a border. Exactly two vertices will have odd degree: the vertices for Nevada and Utah. Thus you must start your road trip at in one of those states and end it in the other.

Which of the following graphs contain an Euler path? Which contain an Euler circuit?

• \(K_5\text{.}\)
• \(K_{5,7}\)
• \(K_{2,7}\)
• \(K_4\) does not have an Euler path or circuit.
• \(K_5\) has an Euler circuit (so also an Euler path).
• \(K_{5,7}\) does not have an Euler path or circuit.
• \(K_{2,7}\) has an Euler path but not an Euler circuit.
• \(C_7\) has an Euler circuit (it is a circuit graph!)
• \(P_7\) has an Euler path but no Euler circuit.

Edward A. Mouse has just finished his brand new house. The floor plan is shown below:

Edward wants to give a tour of his new pad to a lady-mouse-friend. Is it possible for them to walk through every doorway exactly once? If so, in which rooms must they begin and end the tour? Explain.

Is it possible to tour the house visiting each room exactly once (not necessarily using every doorway)? Explain.

After a few mouse-years, Edward decides to remodel. He would like to add some new doors between the rooms he has. Of course, he cannot add any doors to the exterior of the house. Is it possible for each room to have an odd number of doors? Explain.

For which \(n\) does the graph \(K_n\) contain an Euler circuit? Explain.

When \(n\) is odd, \(K_n\) contains an Euler circuit. This is because every vertex has degree \(n-1\text{,}\) so an odd \(n\) results in all degrees being even.

For which \(m\) and \(n\) does the graph \(K_{m,n}\) contain an Euler path? An Euler circuit? Explain.

If both \(m\) and \(n\) are even, then \(K_{m,n}\) has an Euler circuit. When both are odd, there is no Euler path or circuit. If one is 2 and the other is odd, then there is an Euler path but not an Euler circuit.

For which \(n\) does \(K_n\) contain a Hamilton path? A Hamilton cycle? Explain.

All values of \(n\text{.}\) In particular, \(K_n\) contains \(C_n\) as a subgroup, which is a cycle that includes every vertex.

For which \(m\) and \(n\) does the graph \(K_{m,n}\) contain a Hamilton path? A Hamilton cycle? Explain.

As long as \(|m-n| \le 1\text{,}\) the graph \(K_{m,n}\) will have a Hamilton path. To have a Hamilton cycle, we must have \(m=n\text{.}\)

A bridge builder has come to Königsberg and would like to add bridges so that it is possible to travel over every bridge exactly once. How many bridges must be built?

If we build one bridge, we can have an Euler path. Two bridges must be built for an Euler circuit.

Below is a graph representing friendships between a group of students (each vertex is a student and each edge is a friendship). Is it possible for the students to sit around a round table in such a way that every student sits between two friends? What does this question have to do with paths?

We are looking for a Hamiltonian cycle, and this graph does have one:

Suppose a graph has a Hamilton path. What is the maximum number of vertices of degree one the graph can have? Explain why your answer is correct.

Find a graph which does not have a Hamilton path even though no vertex has degree one. Explain why your example works.

Consider the following graph:

• Find a Hamilton path. Can your path be extended to a Hamilton cycle?
• Is the graph bipartite? If so, how many vertices are in each “part”?
• Use your answer to part (b) to prove that the graph has no Hamilton cycle.
• Suppose you have a bipartite graph \(G\) in which one part has at least two more vertices than the other. Prove that \(G\) does not have a Hamilton path.

Module 4: Graph Theory

Euler and hamiltonian paths and circuits, learning outcomes.

• Determine whether a graph has an Euler path and/ or circuit
• Use Fleury’s algorithm to find an Euler circuit
• Add edges to a graph to create an Euler circuit if one doesn’t exist
• Identify whether a graph has a Hamiltonian circuit or path
• Find the optimal Hamiltonian circuit for a graph using the brute force algorithm, the nearest neighbor algorithm, and the sorted edges algorithm
• Identify a connected graph that is a spanning tree
• Use Kruskal’s algorithm to form a spanning tree, and a minimum cost spanning tree

In the next lesson, we will investigate specific kinds of paths through a graph called Euler paths and circuits. Euler paths are an optimal path through a graph. They are named after him because it was Euler who first defined them.

By counting the number of vertices of a graph, and their degree we can determine whether a graph has an Euler path or circuit. We will also learn another algorithm that will allow us to find an Euler circuit once we determine that a graph has one.

Euler Circuits

In the first section, we created a graph of the Königsberg bridges and asked whether it was possible to walk across every bridge once. Because Euler first studied this question, these types of paths are named after him.

An Euler path is a path that uses every edge in a graph with no repeats. Being a path, it does not have to return to the starting vertex.

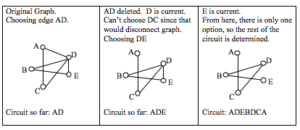
In the graph shown below, there are several Euler paths. One such path is CABDCB. The path is shown in arrows to the right, with the order of edges numbered.

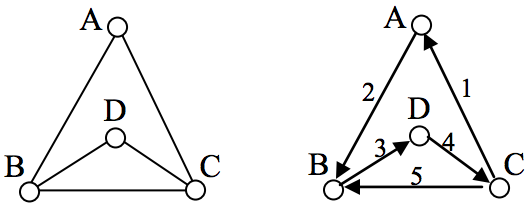
Euler Circuit

An Euler circuit is a circuit that uses every edge in a graph with no repeats. Being a circuit, it must start and end at the same vertex.

The graph below has several possible Euler circuits. Here’s a couple, starting and ending at vertex A: ADEACEFCBA and AECABCFEDA. The second is shown in arrows.

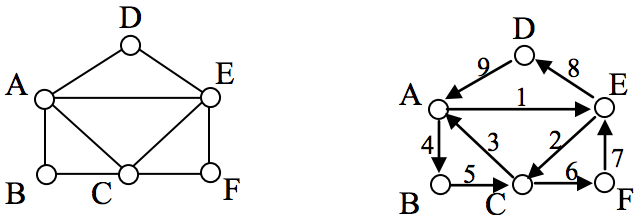
Look back at the example used for Euler paths—does that graph have an Euler circuit? A few tries will tell you no; that graph does not have an Euler circuit. When we were working with shortest paths, we were interested in the optimal path. With Euler paths and circuits, we’re primarily interested in whether an Euler path or circuit exists .

Why do we care if an Euler circuit exists? Think back to our housing development lawn inspector from the beginning of the chapter. The lawn inspector is interested in walking as little as possible. The ideal situation would be a circuit that covers every street with no repeats. That’s an Euler circuit! Luckily, Euler solved the question of whether or not an Euler path or circuit will exist.

Euler’s Path and Circuit Theorems

A graph will contain an Euler path if it contains at most two vertices of odd degree.

A graph will contain an Euler circuit if all vertices have even degree

In the graph below, vertices A and C have degree 4, since there are 4 edges leading into each vertex. B is degree 2, D is degree 3, and E is degree 1. This graph contains two vertices with odd degree (D and E) and three vertices with even degree (A, B, and C), so Euler’s theorems tell us this graph has an Euler path, but not an Euler circuit.

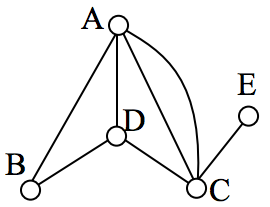
Is there an Euler circuit on the housing development lawn inspector graph we created earlier in the chapter? All the highlighted vertices have odd degree. Since there are more than two vertices with odd degree, there are no Euler paths or Euler circuits on this graph. Unfortunately our lawn inspector will need to do some backtracking.

When it snows in the same housing development, the snowplow has to plow both sides of every street. For simplicity, we’ll assume the plow is out early enough that it can ignore traffic laws and drive down either side of the street in either direction. This can be visualized in the graph by drawing two edges for each street, representing the two sides of the street.

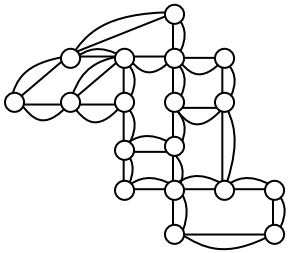
Notice that every vertex in this graph has even degree, so this graph does have an Euler circuit.

The following video gives more examples of how to determine an Euler path, and an Euler Circuit for a graph.

Fleury’s Algorithm

Fleury’s algorithm.

Find an Euler Circuit on this graph using Fleury’s algorithm, starting at vertex A.

Does the graph below have an Euler Circuit? If so, find one.

The following video presents more examples of using Fleury’s algorithm to find an Euler Circuit.

Eulerization and the Chinese Postman Problem

Not every graph has an Euler path or circuit, yet our lawn inspector still needs to do her inspections. Her goal is to minimize the amount of walking she has to do. In order to do that, she will have to duplicate some edges in the graph until an Euler circuit exists.

Eulerization

Eulerization is the process of adding edges to a graph to create an Euler circuit on a graph. To eulerize a graph, edges are duplicated to connect pairs of vertices with odd degree. Connecting two odd degree vertices increases the degree of each, giving them both even degree. When two odd degree vertices are not directly connected, we can duplicate all edges in a path connecting the two.

Note that we can only duplicate edges, not create edges where there wasn’t one before. Duplicating edges would mean walking or driving down a road twice, while creating an edge where there wasn’t one before is akin to installing a new road!

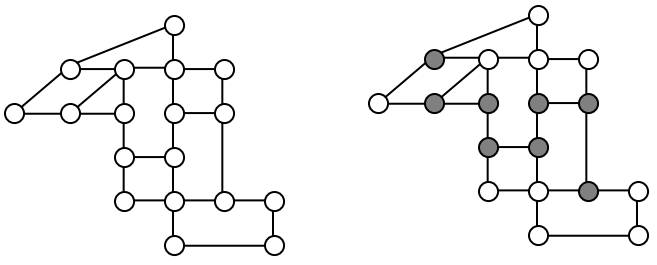
For the rectangular graph shown, three possible eulerizations are shown. Notice in each of these cases the vertices that started with odd degrees have even degrees after eulerization, allowing for an Euler circuit.

In the example above, you’ll notice that the last eulerization required duplicating seven edges, while the first two only required duplicating five edges. If we were eulerizing the graph to find a walking path, we would want the eulerization with minimal duplications. If the edges had weights representing distances or costs, then we would want to select the eulerization with the minimal total added weight.

Eulerize the graph shown, then find an Euler circuit on the eulerized graph.

Looking again at the graph for our lawn inspector from Examples 1 and 8, the vertices with odd degree are shown highlighted. With eight vertices, we will always have to duplicate at least four edges. In this case, we need to duplicate five edges since two odd degree vertices are not directly connected. Without weights we can’t be certain this is the eulerization that minimizes walking distance, but it looks pretty good.

The problem of finding the optimal eulerization is called the Chinese Postman Problem, a name given by an American in honor of the Chinese mathematician Mei-Ko Kwan who first studied the problem in 1962 while trying to find optimal delivery routes for postal carriers.  This problem is important in determining efficient routes for garbage trucks, school buses, parking meter checkers, street sweepers, and more.

Unfortunately, algorithms to solve this problem are fairly complex. Some simpler cases are considered in the exercises

The following video shows another view of finding an Eulerization of the lawn inspector problem.

Hamiltonian Circuits

The traveling salesman problem.

In the last section, we considered optimizing a walking route for a postal carrier. How is this different than the requirements of a package delivery driver? While the postal carrier needed to walk down every street (edge) to deliver the mail, the package delivery driver instead needs to visit every one of a set of delivery locations. Instead of looking for a circuit that covers every edge once, the package deliverer is interested in a circuit that visits every vertex once.

Hamiltonian Circuits and Paths

A Hamiltonian circuit is a circuit that visits every vertex once with no repeats. Being a circuit, it must start and end at the same vertex. A Hamiltonian path also visits every vertex once with no repeats, but does not have to start and end at the same vertex.

Hamiltonian circuits are named for William Rowan Hamilton who studied them in the 1800’s.

One Hamiltonian circuit is shown on the graph below. There are several other Hamiltonian circuits possible on this graph. Notice that the circuit only has to visit every vertex once; it does not need to use every edge.

This circuit could be notated by the sequence of vertices visited, starting and ending at the same vertex: ABFGCDHMLKJEA. Notice that the same circuit could be written in reverse order, or starting and ending at a different vertex.

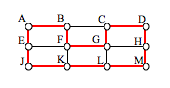
Unlike with Euler circuits, there is no nice theorem that allows us to instantly determine whether or not a Hamiltonian circuit exists for all graphs. [1]

Does a Hamiltonian path or circuit exist on the graph below?

We can see that once we travel to vertex E there is no way to leave without returning to C, so there is no possibility of a Hamiltonian circuit. If we start at vertex E we can find several Hamiltonian paths, such as ECDAB and ECABD

With Hamiltonian circuits, our focus will not be on existence, but on the question of optimization; given a graph where the edges have weights, can we find the optimal Hamiltonian circuit; the one with lowest total weight.

Watch this video to see the examples above worked out.

This problem is called the Traveling salesman problem (TSP) because the question can be framed like this: Suppose a salesman needs to give sales pitches in four cities. He looks up the airfares between each city, and puts the costs in a graph. In what order should he travel to visit each city once then return home with the lowest cost?

To answer this question of how to find the lowest cost Hamiltonian circuit, we will consider some possible approaches. The first option that might come to mind is to just try all different possible circuits.

question can be framed like this: Suppose a salesman needs to give sales pitches in four cities. He looks up the airfares between each city, and puts the costs in a graph. In what order should he travel to visit each city once then return home with the lowest cost?

Brute Force Algorithm (a.k.a. exhaustive search)

1.     List all possible Hamiltonian circuits

2.     Find the length of each circuit by adding the edge weights

3.     Select the circuit with minimal total weight.

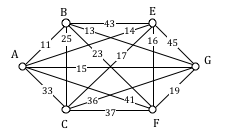
Apply the Brute force algorithm to find the minimum cost Hamiltonian circuit on the graph below.

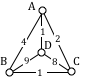
To apply the Brute force algorithm, we list all possible Hamiltonian circuits and calculate their weight:

Note: These are the unique circuits on this graph. All other possible circuits are the reverse of the listed ones or start at a different vertex, but result in the same weights.

From this we can see that the second circuit, ABDCA, is the optimal circuit.

Watch these examples worked again in the following video.

The Brute force algorithm is optimal; it will always produce the Hamiltonian circuit with minimum weight. Is it efficient? To answer that question, we need to consider how many Hamiltonian circuits a graph could have. For simplicity, let’s look at the worst-case possibility, where every vertex is connected to every other vertex. This is called a complete graph.

Suppose we had a complete graph with five vertices like the air travel graph above. From Seattle there are four cities we can visit first. From each of those, there are three choices. From each of those cities, there are two possible cities to visit next. There is then only one choice for the last city before returning home.

This can be shown visually:

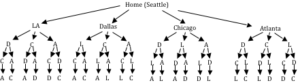
Counting the number of routes, we can see thereare [latex]4\cdot{3}\cdot{2}\cdot{1}[/latex] routes. For six cities there would be [latex]5\cdot{4}\cdot{3}\cdot{2}\cdot{1}[/latex] routes.

Number of Possible Circuits

For N vertices in a complete graph, there will be [latex](n-1)!=(n-1)(n-2)(n-3)\dots{3}\cdot{2}\cdot{1}[/latex] routes. Half of these are duplicates in reverse order, so there are [latex]\frac{(n-1)!}{2}[/latex] unique circuits.

The exclamation symbol, !, is read “factorial” and is shorthand for the product shown.

How many circuits would a complete graph with 8 vertices have?

A complete graph with 8 vertices would have = 5040 possible Hamiltonian circuits. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes.

While this is a lot, it doesn’t seem unreasonably huge. But consider what happens as the number of cities increase:

As you can see the number of circuits is growing extremely quickly. If a computer looked at one billion circuits a second, it would still take almost two years to examine all the possible circuits with only 20 cities! Certainly Brute Force is not an efficient algorithm.

Nearest Neighbor Algorithm (NNA)

1.     Select a starting point.

2.     Move to the nearest unvisited vertex (the edge with smallest weight).

3.     Repeat until the circuit is complete.

Unfortunately, no one has yet found an efficient and optimal algorithm to solve the TSP, and it is very unlikely anyone ever will. Since it is not practical to use brute force to solve the problem, we turn instead to heuristic algorithms ; efficient algorithms that give approximate solutions. In other words, heuristic algorithms are fast, but may or may not produce the optimal circuit.

Consider our earlier graph, shown to the right.

Starting at vertex A, the nearest neighbor is vertex D with a weight of 1.

From D, the nearest neighbor is C, with a weight of 8.

From C, our only option is to move to vertex B, the only unvisited vertex, with a cost of 13.

From B we return to A with a weight of 4.

The resulting circuit is ADCBA with a total weight of [latex]1+8+13+4 = 26[/latex].

Watch the example worked out in the following video.

We ended up finding the worst circuit in the graph! What happened? Unfortunately, while it is very easy to implement, the NNA is a greedy algorithm, meaning it only looks at the immediate decision without considering the consequences in the future. In this case, following the edge AD forced us to use the very expensive edge BC later.

Consider again our salesman. Starting in Seattle, the nearest neighbor (cheapest flight) is to LA, at a cost of $70. From there:

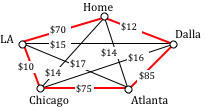
LA to Chicago: $100

Chicago to Atlanta: $75

Atlanta to Dallas: $85

Dallas to Seattle: $120

Total cost: $450

In this case, nearest neighbor did find the optimal circuit.

Watch this example worked out again in this video.

Going back to our first example, how could we improve the outcome? One option would be to redo the nearest neighbor algorithm with a different starting point to see if the result changed. Since nearest neighbor is so fast, doing it several times isn’t a big deal.

We will revisit the graph from Example 17.

Starting at vertex A resulted in a circuit with weight 26.

Starting at vertex B, the nearest neighbor circuit is BADCB with a weight of 4+1+8+13 = 26. This is the same circuit we found starting at vertex A. No better.

Starting at vertex C, the nearest neighbor circuit is CADBC with a weight of 2+1+9+13 = 25. Better!

Starting at vertex D, the nearest neighbor circuit is DACBA. Notice that this is actually the same circuit we found starting at C, just written with a different starting vertex.

The RNNA was able to produce a slightly better circuit with a weight of 25, but still not the optimal circuit in this case. Notice that even though we found the circuit by starting at vertex C, we could still write the circuit starting at A: ADBCA or ACBDA.

The table below shows the time, in milliseconds, it takes to send a packet of data between computers on a network. If data needed to be sent in sequence to each computer, then notification needed to come back to the original computer, we would be solving the TSP. The computers are labeled A-F for convenience.

a.     Find the circuit generated by the NNA starting at vertex B.

b.     Find the circuit generated by the RNNA.

While certainly better than the basic NNA, unfortunately, the RNNA is still greedy and will produce very bad results for some graphs. As an alternative, our next approach will step back and look at the “big picture” – it will select first the edges that are shortest, and then fill in the gaps.

Using the four vertex graph from earlier, we can use the Sorted Edges algorithm.

The cheapest edge is AD, with a cost of 1. We highlight that edge to mark it selected.

The next shortest edge is AC, with a weight of 2, so we highlight that edge.

For the third edge, we’d like to add AB, but that would give vertex A degree 3, which is not allowed in a Hamiltonian circuit. The next shortest edge is CD, but that edge would create a circuit ACDA that does not include vertex B, so we reject that edge. The next shortest edge is BD, so we add that edge to the graph.

We then add the last edge to complete the circuit: ACBDA with weight 25.

Notice that the algorithm did not produce the optimal circuit in this case; the optimal circuit is ACDBA with weight 23.

While the Sorted Edge algorithm overcomes some of the shortcomings of NNA, it is still only a heuristic algorithm, and does not guarantee the optimal circuit.

Your teacher’s band, Derivative Work , is doing a bar tour in Oregon. The driving distances are shown below. Plan an efficient route for your teacher to visit all the cities and return to the starting location. Use NNA starting at Portland, and then use Sorted Edges.

To see the entire table, scroll to the right

Using NNA with a large number of cities, you might find it helpful to mark off the cities as they’re visited to keep from accidently visiting them again. Looking in the row for Portland, the smallest distance is 47, to Salem. Following that idea, our circuit will be:

Portland to Salem                    47

Salem to Corvallis                   40

Corvallis to Eugene                 47

Eugene to Newport                 91

Newport to Seaside                117

Seaside to Astoria                   17

Astoria to Bend                      255

Bend to Ashland                     200

Ashland to Crater Lake           108

Crater Lake to Portland          344

Total trip length:                     1266 miles

Using Sorted Edges, you might find it helpful to draw an empty graph, perhaps by drawing vertices in a circular pattern. Adding edges to the graph as you select them will help you visualize any circuits or vertices with degree 3.

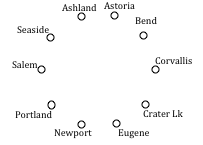
We start adding the shortest edges:

Seaside to Astoria       17 miles

Corvallis to Salem       40 miles

Portland to Salem        47 miles

Corvallis to Eugene     47 miles

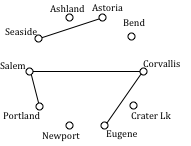
The graph after adding these edges is shown to the right.   The next shortest edge is from Corvallis to Newport at 52 miles, but adding that edge would give Corvallis degree 3.

Continuing on, we can skip over any edge pair that contains Salem or Corvallis, since they both already have degree 2.

Portland to Seaside                 78 miles

Eugene to Newport                 91 miles

Portland to Astoria                 (reject – closes circuit)

Ashland to Crater Lk  108 miles

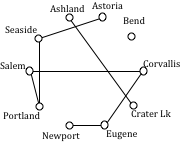
The graph after adding these edges is shown to the right. At this point, we can skip over any edge pair that contains Salem, Seaside, Eugene, Portland, or Corvallis since they already have degree 2.

Newport to Astoria                (reject – closes circuit)

Newport to Bend                    180 miles

Bend to Ashland                     200 miles

At this point the only way to complete the circuit is to add:

Crater Lk to Astoria   433 miles.  The final circuit, written to start at Portland, is:

Portland, Salem, Corvallis, Eugene, Newport, Bend, Ashland, Crater Lake, Astoria, Seaside, Portland.  Total trip length: 1241 miles.

While better than the NNA route, neither algorithm produced the optimal route. The following route can make the tour in 1069 miles:

Portland, Astoria, Seaside, Newport, Corvallis, Eugene, Ashland, Crater Lake, Bend, Salem, Portland

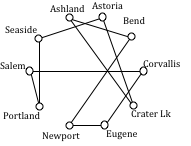
Watch the example of nearest neighbor algorithm for traveling from city to city using a table worked out in the video below.

In the next video we use the same table, but use sorted edges to plan the trip.

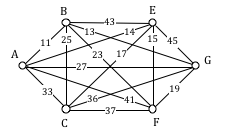
Find the circuit produced by the Sorted Edges algorithm using the graph below.

 Spanning Trees

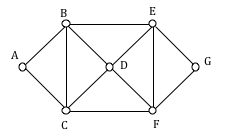
A company requires reliable internet and phone connectivity between their five offices (named A, B, C, D, and E for simplicity) in New York, so they decide to lease dedicated lines from the phone company. The phone company will charge for each link made. The costs, in thousands of dollars per year, are shown in the graph.

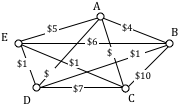
In this case, we don’t need to find a circuit, or even a specific path; all we need to do is make sure we can make a call from any office to any other. In other words, we need to be sure there is a path from any vertex to any other vertex.

Spanning Tree

A spanning tree is a connected graph using all vertices in which there are no circuits.

In other words, there is a path from any vertex to any other vertex, but no circuits.

Some examples of spanning trees are shown below. Notice there are no circuits in the trees, and it is fine to have vertices with degree higher than two.

Usually we have a starting graph to work from, like in the phone example above. In this case, we form our spanning tree by finding a subgraph – a new graph formed using all the vertices but only some of the edges from the original graph. No edges will be created where they didn’t already exist.

Of course, any random spanning tree isn’t really what we want. We want the minimum cost spanning tree (MCST) .

Minimum Cost Spanning Tree (MCST)

The minimum cost spanning tree is the spanning tree with the smallest total edge weight.

A nearest neighbor style approach doesn’t make as much sense here since we don’t need a circuit, so instead we will take an approach similar to sorted edges.

Kruskal’s Algorithm

• Select the cheapest unused edge in the graph.
• Repeat step 1, adding the cheapest unused edge, unless:
• adding the edge would create a circuit

Repeat until a spanning tree is formed

Using our phone line graph from above, begin adding edges:

AB      $4        OK

AE       $5        OK

BE       $6        reject – closes circuit ABEA

DC      $7        OK

AC      $8        OK

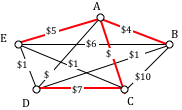
At this point we stop – every vertex is now connected, so we have formed a spanning tree with cost $24 thousand a year.

Remarkably, Kruskal’s algorithm is both optimal and efficient; we are guaranteed to always produce the optimal MCST.

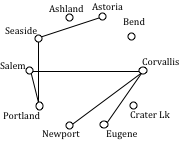
The power company needs to lay updated distribution lines connecting the ten Oregon cities below to the power grid. How can they minimize the amount of new line to lay?

Using Kruskal’s algorithm, we add edges from cheapest to most expensive, rejecting any that close a circuit. We stop when the graph is connected.

Seaside to Astoria                   17 milesCorvallis to Salem                   40 miles

Portland to Salem                    47 miles

Corvallis to Eugene                 47 miles

Corvallis to Newport              52 miles

Salem to Eugene           reject – closes circuit

Portland to Seaside                 78 miles

The graph up to this point is shown below.

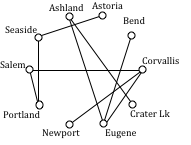
Continuing,

Newport to Salem                   reject

Corvallis to Portland               reject

Eugene to Newport                 reject

Portland to Astoria                 reject

Ashland to Crater Lk              108 miles

Eugene to Portland                  reject

Newport to Portland              reject

Newport to Seaside                reject

Salem to Seaside                      reject

Bend to Eugene                       128 miles

Bend to Salem                         reject

Astoria to Newport                reject

Salem to Astoria                     reject

Corvallis to Seaside                 reject

Portland to Bend                     reject

Astoria to Corvallis                reject

Eugene to Ashland                  178 miles

This connects the graph. The total length of cable to lay would be 695 miles.

Watch the example above worked out in the following video, without a table.

Now we present the same example, with a table in the following video.

Find a minimum cost spanning tree on the graph below using Kruskal’s algorithm.

[1] There are some theorems that can be used in specific circumstances, such as Dirac’s theorem, which says that a Hamiltonian circuit must exist on a graph with n vertices if each vertex has degree n /2 or greater.

• Revision and Adaptaion. Provided by : Lumen Learning. License : CC BY: Attribution
• Learning Outcomes and Introduction. Provided by : Lumen Learning. License : CC BY: Attribution
• Graph Theory: Euler Paths and Euler Circuits . Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/5M-m62qTR-s . License : CC BY: Attribution
• Math in Society. Authored by : Lippman, David. License : CC BY: Attribution
• Graph Theory: Fleury's Algorthim . Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/vvP4Fg4r-Ns . License : CC BY: Attribution
• Hamiltonian circuits. Authored by : OCLPhase2. Located at : https://youtu.be/lUqCtywkskU . License : CC BY: Attribution
• Hamiltonian circuits . Authored by : David Lippman. Located at : https://youtu.be/SjtVuw4-1Qo . License : CC BY: Attribution
• TSP by brute force . Authored by : OCLPhase2. Located at : https://youtu.be/wDXQ6tWsJxw . License : CC BY: Attribution
• Number of circuits in a complete graph . Authored by : OCLPhase2. Located at : https://youtu.be/DwZw4t0qxuQ . License : CC BY: Attribution
• Nearest Neighbor ex2 . Authored by : OCLPhase2. Located at : https://youtu.be/3Eq36iqjGKI . License : CC BY: Attribution
• Sorted Edges ex 2 . Authored by : OCLPhase2. Located at : https://youtu.be/QxF23w3DpQc . License : CC BY: Attribution
• Kruskal's ex 1 . Authored by : OCLPhase2. Located at : https://youtu.be/gaXM0HNErc4 . License : CC BY: Attribution
• Kruskal's from a table . Authored by : OCLPhase2. Located at : https://youtu.be/Pu2_2ftkwdo . License : CC BY: Attribution

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.7: Euler Trails

• Last updated
• Save as PDF
• Page ID 129674

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

After completing this section, you should be able to:

• Describe and identify Euler trails.
• Solve applications using Euler trails theorem.
• Identify bridges in a graph.
• Apply Fleury’s algorithm.
• Evaluate Euler trails in real-world applications.

We used Euler circuits to help us solve problems in which we needed a route that started and ended at the same place. In many applications, it is not necessary for the route to end where it began. In other words, we may not be looking at circuits, but trails, like the old Pony Express trail that led from Sacramento, California in the west to St. Joseph, Missouri in the east, never backtracking.

Euler Trails

If we need a trail that visits every edge in a graph, this would be called an Euler trail . Since trails are walks that do not repeat edges, an Euler trail visits every edge exactly once.

Example 12.29

Recognizing euler trails.

Use Figure 12.150 to determine if each series of vertices represents a trail, an Euler trail, both, or neither. Explain your reasoning.

• a → b → e → g → f → c → d → e
• a → b → e → g → f → c → d → e → b → a → d → g
• g → d → a → b → e → d → c → f → g → e
• It is a trail only. It is a trail because it is a walk that doesn’t cover any edges twice, but it is not an Euler trail because it didn’t cover edges ad or dg .
• It is neither. It is not a trail because it visits ab and be twice. Since it is not a trail, it cannot be an Euler trail.
• It is both. It is a trail because it is a walk that doesn’t cover any edges twice, and it is an Euler trail because it visits all the edges.

Your Turn 12.29

The Five Rooms Puzzle

Just as Euler determined that only graphs with vertices of even degree have Euler circuits, he also realized that the only vertices of odd degree in a graph with an Euler trail are the starting and ending vertices. For example, in Figure 12.150, Graph H has exactly two vertices of odd degree, vertex g and vertex e . Notice the Euler trail we saw in Excercise 3 of Example 12.29 began at vertex g and ended at vertex e .

This is consistent with what we learned about vertices off odd degree when we were studying Euler circuits. We saw that a vertex of odd degree couldn't exist in an Euler circuit as depicted in Figure 12.152. If it was a starting vertex, at some point we would leave the vertex and not be able to return without repeating an edge. If it was not a starting vertex, at some point we would return and not be able to leave without repeating an edge. Since the starting and ending vertices in an Euler trail are not the same, the start is a vertex we want to leave without returning, and the end is a vertex we want to return to and never leave. Those two vertices must have odd degree, but the others cannot.

Let’s use the Euler trail theorem to solve a puzzle so you can amaze your friends! This puzzle is called the “Five Rooms Puzzle.” Suppose that you were in a house with five rooms and the exterior. There is a doorway in every shared wall between any two rooms and between any room and the exterior as shown in Figure 12.153 . Could you find a route through the house that passes through each doorway exactly once?

Let’s represent the puzzle with a graph in which vertices are rooms (or the exterior) and an edge indicates a door between two rooms as shown in Figure 12.154.

To pass through each doorway exactly once means that we cross every edge in the graph exactly once. Since we have not been asked to start and end at the same position, but to visit each edge exactly once, we are looking for an Euler trail. Let’s check the degrees of the vertices.

Since there are more than two vertices of odd degree as shown in Figure 12.155, the graph of the five rooms puzzle contains no Euler path. Now you can amaze and astonish your friends!

Bridges and Local Bridges

Now that we know which graphs have Euler trails, let’s work on a method to find them. The method we will use involves identifying bridges in our graphs. A bridge is an edge which, if removed, increases the number of components in a graph. Bridges are often referred to as cut-edges. In Figure 12.156, there are several examples of bridges. Notice that an edge that is not part of a cycle is always a bridge, and an edge that is part of a cycle is never a bridge.

Edges bf , cg , and dg are “bridges”

The graph in Figure 12.156 is connected, which means it has exactly one component. Each time we remove one of the bridges from the graph the number of components increases by one as shown in Figure 12.157. If we remove all three, the resulting graph in Figure 12.157 has four components.

In sociology, bridges are a key part of social network analysis. Sociologists study two kinds of bridges: local bridges and regular bridges. Regular bridges are defined the same in sociology as in graph theory, but they are unusual when studying a large social network because it is very unlikely a group of individuals in a large social network has only one link to the rest of the network. On the other hand, a local bridge occurs much more frequently. A local bridge is a friendship between two individuals who have no other friends in common. If they lose touch, there is no single individual who can pass information between them. In graph theory, a local bridge is an edge between two vertices, which, when removed, increases the length of the shortest path between its vertices to more than two edges. In Figure 12.158 , a local bridge between vertices b and e has been removed. As a result, the shortest path between b and e is b → i → j → k → e , which is four edges. On the other hand, if edge ab were removed, then there are still paths between a and b that cover only two edges, like a → i → b .

The significance of a local bridge in sociology is that it is the shortest communication route between two groups of people. If the local bridge is removed, the flow of information from one group to another becomes more difficult. Let’s say that vertex b is Brielle and vertex e is Ella. Now, Brielle is less likely to hear about things like job opportunities, that Ella many know about. This is likely to impact Brielle as well as the friends of Brielle.

Example 12.30

Identifying bridges and local bridges.

Use the graph of a social network in Figure 12.159 to answer each question.

• Identify any bridges.
• If all bridges were removed, how many components would there be in the resulting graph?
• Identify one local bridge.
• For the local bridge you identified in part 3, identify the shortest path between the vertices of the local bridge if the local bridge were removed.
• The edges ku, gh , and hi are bridges.

• Three local bridges are dn, ef , and qt , among others.
• If dn were removed, the shortest path between d and n would be d → e → f → j → o → m → n .

Your Turn 12.30

Bridges and Local Bridges in Graph Theory

Finding an Euler Trail with Fleury’s Algorithm

Now that we are familiar with bridges, we can use a technique called Fleury’s algorithm , which is a series of steps, or algorithm, used to find an Euler trail in any graph that has exactly two vertices of odd degree. Here are the steps involved in applying Fleury’s algorithm.

Here are the steps involved in applying Fleury’s algorithm.

Step 1: Begin at either of the two vertices of odd degree.

Step 2: Remove an edge between the vertex and any adjacent vertex that is NOT a bridge, unless there is no other choice, making a note of the edge you removed. Repeat this step until all edges are removed.

Step 3: Write out the Euler trail using the sequence of vertices and edges that you found. For example, if you removed ab, bc, cd, de , and ef , in that order, then the Euler trail is a → b → c → d → e → f .

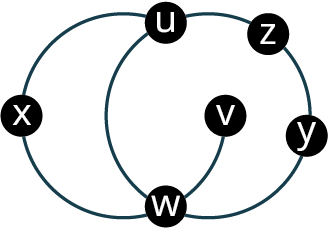
Figure 12.161 shows the steps to find an Euler trail in a graph using Fleury’s algorithm.

The Euler trail that was found in Figure 12.161 is t → v → w → u → t → w → y → x → v .

Example 12.31

Use Fleury’s Algorithm to find an Euler trail for Graph J in Figure 12.162 .

Step 1: Choose one of the two vertices of odd degree, c or f , as your starting vertex. We will choose c .

Step 2: Remove edge ca, cb , or cd . None of these are cut edges so we can select any of the three. We will choose cb as shown in Figure 12.163 to be the first edge removed.

Repeat Step 2 The next choice is to remove edge ba, bd , or bf as shown in Figure 12.163, but bf is not an option since it is a bridge. We will choose ba as shown in Figure 12.164 to be the second edge removed.

Repeat Step 2 for the third, fourth, fifth, sixth, and seventh edges. As shown in Figure 12.164 , until we get to the seventh edge there is only one option each time, ac, cd, db , and bf in that order. For the seventh edge, we must choose between fe and fg . Neither of these are bridges. We choose fe . Figure 12.165 shows that ac, cd, db, bf, and fe have been removed.

Repeat Step 2 for the eight, ninth, tenth, and eleventh edges. As shown in Figure 12.165, there is only one option for each of these edges, eh, hi, ig , and gf , in that order.

Step 3: Write out the Euler trail using the vertices in the sequence that the edges were removed. We removed cb, ba, ac, cd, db, bf, fe, eh, hi, ig , and gf , in that order. The Euler trail is c → b → a → c → d → b → f → e → h → i → g → f .

TIP! To avoid errors, count the number of edges in your graph and make sure thatyour Euler trail represents that number of edges.

Your Turn 12.31

In the previous section, we found Euler circuits using an algorithm that involved joining circuits together into one large circuit. You can also use Fleury’s algorithm to find Euler circuits in any graph with vertices of all even degree. In that case, you can start at any vertex that you would like to use.

Step 1: Begin at any vertex.

Step 3: Write out the Euler circuit using the sequence of vertices and edges that you found. For example, if you removed ab, bc, cd, de , and ea , in that order, then the Euler circuit is a → b → c → d → e → a .

Fluery's Algorithm to Find an Euler Circuit

IMPORTANT! Since a circuit is a closed trail, every Euler circuit is also an Euler trail, but when we say Euler trail in this chapter, we are referring to an open Euler trail that begins and ends at different vertices.

Example 12.32

Finding an euler circuit or euler trail using fleury’s algorithm.

Use Fleury’s algorithm to find either an Euler circuit or Euler trail in Graph G in Figure 12.167 .

Graph G has all vertices of even degree so it has an Euler circuit.

Step 1: Choose any vertex. We will choose vertex j .

Step 2: Remove one of the four edges that meet at vertex j . Since jn is a bridge, we must remove either jh, ji , or jk. We remove ji as shown in Figure 12.168.

Repeat Step 2: Since id is a bridge, we can remove either ih or ik next. We remove ih , and then the only option is to remove hj as shown in Figure 12.169 .

Repeat Step 2: Since jn is a bridge, the next edge removed must be jk , and then the only option is to remove ki followed by id as shown in Figure 12.169 . Even though id is a bridge, it can be removed because it is the only option at this point. Figure 12.170 shows Graph G with these additional edges removed.

Repeat Step 2: Choose any one of the edges db, dc , or de . We remove dc as shown in Figure 12.171.

Repeat Step 2: Since co is a bridge, choose cb next. We remove cb , then bd , and then de as shown in Figure 12.172 .

Repeat Step 2: Next, remove ec and co . Then choose any of op, pn , or om . We remove on as shown in Figure 12.173.

Repeat Step 2: Next, remove either nm , np , or nj , but nj is a So, we remove nm as shown in Figure 12.174 .

Repeat Step 2: Next, remove mo, op, pn , and nj . And we are done!

Step 3: Notice that the algorithm brought us back to the vertex where we started, forming an Euler circuit. Write out the Euler circuit:

j → i → h → j → k → i → d → c → b → d → e → c → o → n → m → o → p → n → j

Your Turn 12.32

WORK IT OUT

We have discussed a lot of subtle concepts in this section. Let’s make sure we are all on the same page. Work with a partner to explain why each of the following facts about bridges are true. Support your explanations with definitions and graphs.

• When a bridge is removed from a graph, the number of components increases.
• A bridge is never part of a circuit.
• An edge that is part of a triangle is never a local bridge.

Check Your Understanding

Section 12.6 exercises.

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges

Euler Circuit in a Directed Graph

• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring
• Traveling Salesman Problem (TSP) Implementation
• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Eulerian Path is a path in graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex. 

A graph is said to be eulerian if it has a eulerian cycle. We have discussed eulerian circuit for an undirected graph . In this post, the same is discussed for a directed graph.

For example, the following graph has eulerian cycle as {1, 0, 3, 4, 0, 2, 1} 

How to check if a directed graph is eulerian?  

A directed graph has an eulerian cycle if following conditions are true

• All vertices with nonzero degree belong to a single strongly connected component . 
• In degree is equal to the out degree for every vertex.

We can detect singly connected component using Kosaraju’s DFS based simple algorithm . 

To compare in degree and out-degree, we need to store in degree and out-degree of every vertex. Out degree can be obtained by the size of an adjacency list. In degree can be stored by creating an array of size equal to the number of vertices. 

Following implementations of above approach. 

 Time complexity of the above implementation is O(V + E) as Kosaraju’s algorithm takes O(V + E) time. After running Kosaraju’s algorithm we traverse all vertices and compare in degree with out degree which takes O(V) time. 

Auxiliary Space : O(V), since an extra visited array of size V is required.

See following as an application of this.  Find if the given array of strings can be chained to form a circle .

Please Login to comment...

Similar reads.

• Euler-Circuit
• graph-connectivity
• graph-cycle

Improve your Coding Skills with Practice

What kind of Experience do you want to share?